Combien existe-t-il de parties d’Échecs différentes?

Vous venez d’être défié aux échecs par votre petit neveu de 11 ans qui pense dur comme fer qu’il va vous mettre échec et mat en moins de temps qu’il ne faut pour le dire. Alors que vous sortez le plateau de jeu qui prend la poussière dans votre grenier, vous vous rendez soudain compte que votre dernière partie remonte à une bonne dizaine d’années… Mince. Qu’est ce qui vous a pris d’affirmer que vous étiez un champion d’échecs dans votre enfance? Il faudrait quand même pas que ce p’tit con vous ridiculise devant toute la famille…
Le temps que vous relisiez en cachette les règles du jeu (merde, comment on fait le grand roque, déjà?), amusons-nous à compter le nombre de parties possibles. Cela ne vous aidera en rien à gagner, mais au moins aurez-vous une anecdote amusante à raconter pour faire oublier votre lamentable défaite…
Au début du jeu, le joueur blanc a 20 possibilités qui s’offrent à lui (les 8 pions à avancer d’une ou deux cases + la sortie d’un cavalier avec 2 possibilités chacune). Le joueur noir a, à son tour, 20 possibilités. Rien que pour le premier coup, il existe donc 20*20= 400 possibilités. Jusque là, ça va.
Arrive le deuxième tour. Les possibilités de déplacement se compliquent tout de suite (et sont directement dépendantes du premier coup… logique). Faisons confiance aux chercheurs qui ont calculé que le nombre de possibilités s’élève à… 20.000. C’est à dire qu’il existe 20.000 combinaisons de déplacement différentes. Pas mal.
Dès le troisième tour, on comprend aisément que le cerveau humain n’est plus capable de calculer seul le nombre total de possibilités. Normal, le chiffre devient astronomique !
Nous voilà déjà bloqués dès le troisième coup… Le mathématicien Claude Shannon, lui, a été bien plus fort que nous et est parvenu à aller jusqu’au bout des calculs. Ses conclusions donnent le tournis: 10120 parties différentes possibles! C’est à dire un 1 avec 120 zéros derrière… Je ne vous ferai pas l’affront de l’écrire en entier! En hommage au mathématicien qui mena ces recherches (mort en 2001), il porte le nom de son créateur: le nombre de Shannon. Sachez juste que ce nombre est encore plus grand qu’un googol (unité de mesure qui vaut 10100 et qui a, soit dit au passage, donné son nom au célèbre moteur de recherche Google…)
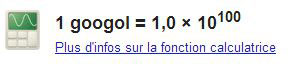
1 Googol, des milliards de milliards de fois plus petits que le nombre de Shannon (Ah! la magie des puissances de 10…)
Un moyen simple de saisir la portée de ce résultat surprenant est le suivant: statistiquement, le nombre moyen de coups joué par partie est de 40. À chaque fois que c’est à son tour de bouger une pièce, le joueur a le choix, en moyenne, entre 30 possibilités. Et ça tombe bien, car (30×30)40 est justement égal au nombre de Shannon…
À titre de comparaison, il y a « seulement » 1080 atomes dans l’Univers… soit 1 milliard de milliard de milliard de milliard fois moins que de parties d’échecs possibles! Impressionnant, non?
– Tonton! Qu’est ce que tu fabriques? Tu viens jouer?
« Ta gueule, p’tit con, tu commences sérieusement à me les briser avec tes échecs à la con », pensez-vous très fort.
– Oui, Kevin, j’arrive, deux secondes!
De grosses gouttes de sueur vous coule le long des tempes. Quelque chose vous dit que vous allez passer un mauvais quart d’heure…

____________________________________
Vous avez aimé cet article ? Alors j'ai besoin de vous ! Vous pouvez soutenir le blog sur Tipeee. Un beau geste, facile à faire, et qui permettra à EtaleTaCulture de garder son indépendance et d'assurer sa survie...
Objectif: 50 donateurs
Récompense: du contenu exclusif et/ou en avant-première
Je vous remercie pour tout le soutien que vous m'apportez depuis maintenant 5 ans, amis lecteurs!
Djinnzz
PS: ça marche aussi en cliquant sur l'image juste en dessous ↓↓↓↓











« il y a « seulement » 1080 atomes dans l’Univers… soit 1 milliard de milliard de milliard de milliard fois moins que de parties d’échecs possibles! »
Je pense plutôt que le chiffre exact est de 10.000 milliards de milliards de milliards de milliards (c’est à dire 10^40, quoi) de fois plus petit.
Curieux de savoir si Kevin va gagner la partie d’échecs ou non ^^
D’où sort le nombre de 10^80 atomes dans l’Univers?
Ca me paraît très petit comme nombre personnellement.
Oui, comme le nombre de parties, c’est complètement faux. On estime sur une partie 40 coups deux heures classiques le nombre de parties à 10^120 soit 10 avec 120 zéros derrière. C’est le nombre de Shannon, mais on estime à environ 10^50 le nombre de positions légales, malheureusement le seul et unique moyen d’avoir une réponse fiable s’obtient par la simulation ce qui serait inutile et très gourmand en calculs…
Bonjour, les articles tirés de la presse scientifique ne manquent pas pour le nombre d’atomes dans l’univers, estimés à 10^80. Par exemple : https://www.science-et-vie.com/ciel-et-espace/sait-on-combien-il-y-a-d-atomes-dans-l-univers-6154
Quant au nombre de Shannon, il existe également pléthore de sites scientifiques qui en parlent. Wikipedia est une bonne entrée en matière : https://fr.wikipedia.org/wiki/Nombre_de_Shannon
Malili:
Le chiffre m’a étionné moi aussi, mais c’est celui qui circule régulièrement sur les sites scientifiques de la toile.
Pour une petite justification que j’ai trouvé:
Vu sur le forum de futura-sciences:
l’Univers est constitué très majoritairement d’hydrogène (vient ensuite l’hélium, etc)… En connaissant le nombre d’atomes dans une étoile (10^57 pour le Soleil), en considérant le nombre d’étoiles (et leurs particularités encore une fois) dans une galaxie (10^11 en moyenne), et le nombre de galaxies dans l’Univers observable (10^11), on peut en déduire le nombre d’atomes.
L’Univers n’est pas seulement constitué d’étoiles, il faut également prendre en compte les nuages de gaz, les atomes répartis ici-ou-là dans le vide, etc.
Tu ajoutes une pincée de corps rocheux, métalliques, et j’en passe (très faible dans la balance) et tu obtiens une soupe de ~10^80 atomes. »
(car 10^57 * 10^11 * 10^11 = 10^(57+11+11) = 10^79 )
Voilà… Du coup, le googol et le nombre de Shannon paraissent encore plus impressionnants quand on sait ça.
Je jour où l’on pourra faire la liste (parmi ces 10^120) des parties gagnantes, il n’y aura plus d’intérêt à jouer aux échecs. Il faudra inventer les échecs chaotiques où le hasard aura sa place 😉
Génial comme article!!!
Surtout la comparaison avec le nombre d’atomes dans l’univers (qui est un nombre fini alors que l’univers est en expansion… je n’y comprendrai jamais rien à tout ce bazar lol).
« le nombre d’atomes dans l’univers (qui est un nombre fini alors que l’univers est en expansion… je n’y comprendrai jamais rien »
Pour expliquer cela, prenons une règle graduée, de 10 cm… c’est à dire 10 petits traits noirs… mettons que l’on étire
cette règle… la règle s’agrandit mais il y a toujours dix petit traits noirs dessus, c’est juste la distance entre deux traits qui augmente…
C’est ce qu’il se passe pour l’univers… C’est comme après un match de foot… Les spectateurs présents dans le stade rentrent chez eux…
Leur nombre n’augmente ni ne diminue, ils s’éloignent juste les uns les autres
Ca sent le vécu le coup du défi par un gamin! 😉
C’est vrai qu’ils peuvent être sacrément doués ces saloperies-là (et après ils se vantent qu’ils ont battu un adulte – y’a des baffes qui se perdent)
Exactement! Dans ce genre de parties, on a tout à perdre, rien à gagner! 😛
#JetaleMaCulture
Le jeu d’échecs est vieux de plusieurs siècles. Les premières traces de ce jeu remontent à 3000 ans avant notre ère, en inde. Ensuite, il a fait son chemin à la Perse, aux arabes, puis à l’Europe. « Shah » est le titre du monarque persan, et automatiquement le roi des échecs a été appelé le Shah.
Pour gagner aux échecs, vous devez vaincre le roi en l’attaquant et en le rendant incapable de bouger. C’est ce qu’on appelle « échec et mat ». Cette expression vient en fait de « Shah Mat » qui signifie « Le roi est vaincu ». Mat est un mot persan pour dire « vaincu », « impuissant », ou « paralysé ».
Cependant, des millions de passionnés d’échecs pensent que « échec et mat » vient de l’expression arabe « al cheikh mat » qui signifie « Le roi est mort ». Par contre, le roi des échecs ne peut pas être « tué », « vaincu » semble avoir beaucoup plus de sens à ce sujet.
le nombre d’atomes dans l’univers n’est qu’une grosse connerie étant donné que l’on ne connait pas les limites de l’univers. Il est soit disant en pleine expansion, l’homme a des certitudes que l’avenir contredira ou pas car l’homme ne pourra jamais savoir la taille de l’univers, la galaxie dans laquelle nous sommes fait 100 millions années lumières et les galaxies, il y en a un paquet (celles que l’on peut voir)…